Backpropagation is the backbone of Deep Learning. Sometime back when I was trying to understand what ‘learning’ is I realized that I didn’t really know much about how backpropagation is actually implemented. I just knew how to do a simple loss.backward(). I soon found out that there is much more to backpropagation than chain rule. ‘Automatic Differentiation’ and ‘Message passing view of Backpropagation’ especially amazed me. When I set out learning in-depth about backpropagation, I couldn’t find everything necessary in one place. Some articles will only cover the basics of backprop, some will lightly touch on autodiff and not discuss autodiff’s basics. I hope this article serves as a good resource for people trying to understand backpropagation and how it’s implemented in modern libraries. Let me know in the comments if I am missing any aspect.
Note:
a) The article may seem math-heavy. To help build intuition, I have supplemented maths with visual elements.
b) The article is not intended as a quick read. However, to keep the main body short, I have used Appendixes for supplementary concepts.
Intro to backprop:
Central to the concept of backprop is the idea of a cost function. Cost functions let us choose what we want to achieve. In most cases, either we want to maximize rewards or we want to minimize errors. Cost function helps to formalize the uncertainty or randomness of our models[check Appendix A]. Once we can formalize randomness, we can use optimization algorithms to reduce it.
Let’s say our model comprises of parameters ![]() and our cost function is
and our cost function is ![]() . So, with gradients
. So, with gradients ![]() we can update the parameters
we can update the parameters ![]() using gradient descent to change
using gradient descent to change ![]() [For more on gradients and gradient descent check Appendix B.
[For more on gradients and gradient descent check Appendix B.
A forward pass in a simple Multilayer Perceptron looks like this:

The above model has ![]() as its trainable parameters. A partial derivative of the cost function with respect to a parameter like
as its trainable parameters. A partial derivative of the cost function with respect to a parameter like ![]() (
(![]() ) tells how minute changes in
) tells how minute changes in ![]() changes the value of
changes the value of ![]() . But,
. But, ![]() doesn’t directly affect the value of cost function. Value of
doesn’t directly affect the value of cost function. Value of ![]() affects the value of output of node 1. This output value later affects outputs of Node 3 and 4. Node 3 and 4 affect Output Node. Output Node directly affects
affects the value of output of node 1. This output value later affects outputs of Node 3 and 4. Node 3 and 4 affect Output Node. Output Node directly affects ![]() . So you can see that the connection between
. So you can see that the connection between ![]() and
and ![]() is kind of a chain with multiple intermediary nodes. So the question comes how do we find the value of
is kind of a chain with multiple intermediary nodes. So the question comes how do we find the value of ![]() ?
?

All the paths that connect a parameter to a cost function contribute in the total derivative of that parameter. In the above case, since there are 2 paths that connect ![]() with
with ![]() ,
, ![]() has two terms:
has two terms:
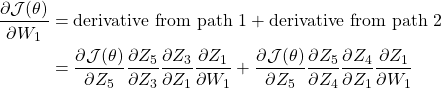
where ![]() is the output of the ith node and considering Node ‘O’ as Node 5. We got the above expression using Chain Rule[check Appendix C].
is the output of the ith node and considering Node ‘O’ as Node 5. We got the above expression using Chain Rule[check Appendix C].
If you look at the gradients of our model parameters, you will notice two fundamental things:
1. To update the value of ![]() we have to save 6 jacobians. For a much deeper network, the number of jacobians we have to save will keep on increasing. It is a big problem because jacobian can very large[Check Appendix D].
we have to save 6 jacobians. For a much deeper network, the number of jacobians we have to save will keep on increasing. It is a big problem because jacobian can very large[Check Appendix D].
2. Repetitions of jacobians: If you check the next gif, you will notice how so many terms are repeated and need to be calculated again and again.
Automatic Differentiation:
Practically, we calculate gradients using Automatic Differentiation or Autodiff or Autograd. We use it in almost all libraries that support Neural Networks because it circumvents the aforementioned problems. Autodiff achieves so by leveraging the computational graph(CG) and converting all operations into primitive operations.
-
Converting Computational graph into primitive operations:
This allows us to reformulate the entire CG in terms of simple functions and basic operations like
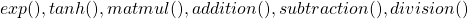 etc. Converting CG into primitive operations is done behind the scenes in Pytorch and Tensorflow. The reason it’s done will soon become clear.
etc. Converting CG into primitive operations is done behind the scenes in Pytorch and Tensorflow. The reason it’s done will soon become clear.We can rewrite operations in our Node 1(
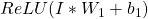 )as:
)as:
where,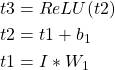
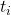 are intermediate nodes with results of primitive operations.
are intermediate nodes with results of primitive operations.
Similarly, for all the nodes, we can rewrite the CG as:

-
Traversing the CG in reverse order
First off, we use a different notation in autodiff. We represent
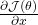 as
as 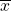 . Autodiff algorithm can be written as:
. Autodiff algorithm can be written as:- Find the value of all primitive nodes in the forward pass.
- In backward pass: Assign last node with a gradient of 1. Iterate through CG in reverse order. Assign each node a gradient
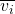 such that:
such that:
where, j are all nodes that use the output value of Node i in forward pass. This rule will become clear once we apply it to our current CG.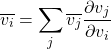

If you want to check out gradients of all parameters computed in the above manner, check out Appendix E.Key properties:
- In autodiff, we iteratively apply the chain rule on each node as opposed to finding the chain rule ‘expression’ for each node.
- Since it passes down gradients there is no repetition in terms.
- If you notice, all gradients are of the form
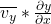 . This avoids costly multiplication of multiple jacobians which as we discussed tend to be huge.
. This avoids costly multiplication of multiple jacobians which as we discussed tend to be huge. - The overall cost of doing backpropagation depends linearly on the time taken to do forward pass.
-
Writing Jacobian Products for primitive operation:
We still haven’t answered why we reformulated our CG down to primitive operations. There are 2 major reasons:
- We can bypass the construction of Jacobians:
As you noticed that in autodiff, the gradients are of the form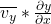 , Multiplication of a vector with Jacobian can still be costly. If we break down our CG into only user-defined primitive functions like
, Multiplication of a vector with Jacobian can still be costly. If we break down our CG into only user-defined primitive functions like  then we can directly return the gradients of nodes. To do so, we use functions called VJP(Vector Jacobian Product) or sometimes JVP(Jacobian Vector product). They directly compute the gradients for a particular primitive node. Eg:
then we can directly return the gradients of nodes. To do so, we use functions called VJP(Vector Jacobian Product) or sometimes JVP(Jacobian Vector product). They directly compute the gradients for a particular primitive node. Eg:
- Let’s take a simple primitive node which does addition:
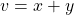 ,
,  is the child node and
is the child node and 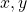 are parent nodes.
are parent nodes. 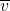 is gradient coming from the child and we want to find
is gradient coming from the child and we want to find 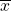 . We know from autodiff algorithm:
. We know from autodiff algorithm:
But the neat trick is that we already know for addition,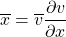
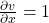 . Thus we can avoid creating a jacobian and its expensive multiplication by directly defining a function that returns
. Thus we can avoid creating a jacobian and its expensive multiplication by directly defining a function that returns 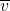 .
.
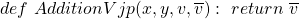
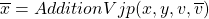
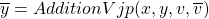
-
A primitive node that does exp():
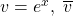 is gradient coming from the child. Then its VJP:
is gradient coming from the child. Then its VJP: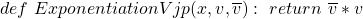
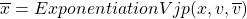
-
A primitive node that does log():
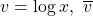 is gradient coming from the child. Then its VJP:
is gradient coming from the child. Then its VJP: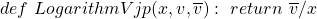
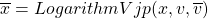
I hope now you understand how these user-defined VJP of primitive operations circumvent costly operations of jacobian construction and its multiplication. A cool thing is that even if we write a complex and composite function, our autodiff library will break the function into corresponding primitive functions and take care of backpropagation using VJPs.
- Let’s take a simple primitive node which does addition:
- If we can break down a CG to its primitive operations and define the corresponding VJP, we have automated backpropagation. Yaaayyyyy!!!!! Well, not so quick, there are many more things we have yet to take care of. First, creating structures that enable the identification of primitive operations. Second, in real-world applications, everything is done using matrices so we will have to take care of matrix calculus as well. But the ability to only worry about the forward pass and let your library take care of the rest is a tremendous boost to productivity.
- We can bypass the construction of Jacobians:
Message passing view of backprop
In this section, we will see how to leverage the recursive nature of backpropagation. Due to this property, we can design architectures containing many modules arranged in any shape as long as these modules follow certain conditions. The backpropagation signal here is similar to ![]() which is passed between parent and child nodes.
which is passed between parent and child nodes.
-
A modular view of architectures:
We can plan our architectures as interconnected modules. Each module has 4 types of signals passing through it:
- Input(
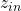 )
) - Output(
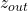 ): A module processes Input and transforms it to give an Output
): A module processes Input and transforms it to give an Output - Incoming Gradients(
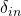 ): During backward pass, these are the gradients coming from children of this module.
): During backward pass, these are the gradients coming from children of this module. - Outgoing Gradients(
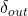 ): During backward pass, these are gradients that a module sends to its parents.
): During backward pass, these are gradients that a module sends to its parents.
A module should atleast have these 3 functions:
- forward(): that converts inputs to outputs of a module
- backward() that finds gradients of outputs wrt to inputs(
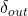 ) of the module
) of the module - parameter_gradients(): which finds gradients of outputs wrt trainable parameters of the module.

And that’s it. Now you can rearrange these modules in different shapes to form any architectures that use backprop. However, we still have not discussed how to formulate backward() and parameter_Gradients() in case of multiple children, and guess what we will use? The good old, Chain Rule.
- Input(
-
Gradient flow between different modules:
The end expression is the same with single or multiple children. But to build intuition, let’s start with a single child.
- Single child:
Let our current module be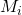 and its child is
and its child is 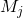 . Here, during backward pass, we have only 1 incoming gradient
. Here, during backward pass, we have only 1 incoming gradient 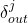 . Then for the functions:
. Then for the functions:
- backward():
Remember backward() finds gradients of outputs wrt to inputs i.e.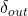 . So from chain rule:
. So from chain rule: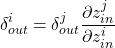
The gradients we send back from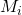 (
(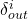 ) is the gradient of module output wrt to its inputs times the gradients module received.
) is the gradient of module output wrt to its inputs times the gradients module received. - parameter_gradients():
Let’s say our module has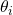 as a trainable parameter. Then gradient of Cost Function
as a trainable parameter. Then gradient of Cost Function 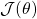 wrt to
wrt to 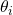 is:
is: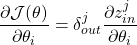
The gradients we use to update our parameters are the gradient of module output wrt to its parameters times the gradients module received.
E.g.: It is similar to gradients we found in the initial MLP example. To find gradients for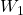 we multiplied the incoming gradients with
we multiplied the incoming gradients with 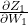
- backward():
- Multiple children:
In case of multiple children, we have to accommodate for gradients received from all the children. The terms we used for a single child become summation over all the children. Let’s say module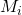 has N children then the functions are:
has N children then the functions are:
- backward() :
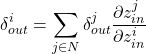
i.e. sum of ((gradients coming from child) times (derivative of (input to that child) wrt (input of Module i))). Note: here we are saying derivative of input to that child because a module might have multiple outputs with different outputs going to different child modules. - parameter_gradients():
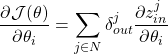
i.e. sum of ((gradients coming from child) times (derivative of (input to that child) wrt (params of Module i))).
- backward() :
- Single child:
Why we discussed the Message passing view of backprop? The reason is that it enables creating very different architectures. I hope the next image sparks your imagination.

Appendix A: Cost Functions
To understand the need for a cost function, we need to understand what learning is. In the context of machine learning and deep learning algorithms, learning means the ability to predict. In our models, we want to reduce the uncertainty or randomness involved in our predictions of the data. We want our predictions to be spot on, not vary with the same inputs. To measure uncertainty in our models we the classical measure of randomness, entropy.
Entropy by definition is:
![]()
here, in the context of machine learning
Let’s see how cost functions reduce the entropy of predictions for different tasks.
For classification tasks:
Let’s task a classification task of n classes using softmax.
So, the probability that a particular sample ![]() is of class n is:
is of class n is:
![]()
where,
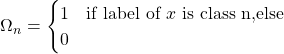
So, our likelihood for one data sample is:
![]()
So entropy of classification for one data sample becomes:
![]()
The above expression may seem daunting but if you notice ![]() is
is ![]() for all non label classes and when
for all non label classes and when ![]() is 1 then the above expression gets it lowest value(
is 1 then the above expression gets it lowest value(![]() ) when the model gives the probability of 1 to the label class which will be a spot on prediction for the label class.
) when the model gives the probability of 1 to the label class which will be a spot on prediction for the label class.
For regression tasks:
The first go to option for regression tasks is MeanSquarredError. But in MSE there is no notion of a ![]() . Another way of setting up a regression task is to learn a probability distribution. This way we can formulate
. Another way of setting up a regression task is to learn a probability distribution. This way we can formulate ![]() and use negative log-likelihood as our cost function. A go to choice is to learn a normal distribution of our logits. We assume that our logits are the mean of that distribution and we find the
and use negative log-likelihood as our cost function. A go to choice is to learn a normal distribution of our logits. We assume that our logits are the mean of that distribution and we find the ![]() using the probability density function(PDF) of the distribution. The idea is then to maximize the probabilities
using the probability density function(PDF) of the distribution. The idea is then to maximize the probabilities ![]() which happens when our logits
which happens when our logits ![]() are equal to the labels
are equal to the labels ![]() i.e.
i.e. ![]() .
.
Using PDF of a normal distribution,
![]()
So our entropy becomes,
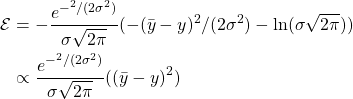
Again, a daunting expression, but it minimizes when ![]()
So, as we saw in both cases, the point of a cost function is to help us to formalize the uncertainty of the model and by improving our predictions we reduce this uncertainty.
Appendix B: Gradients & Gradient Descent
A gradient tells how a function is changing at that particular point. Key points regarding gradients:
1. A gradient shows the direction in which the function is increasing.
2. When gradients are zero, it means our function has reached a peak or a trough.
If we take a small step towards the direction mentioned by a gradient, we move to a point with a function value greater than the previous position. If we take this step again and again, we reach a ‘maxima’ point of that function. This is the basis of many optimization algorithms. Find gradients wrt to cost function and keep updating parameters in the direction of their gradients.
Gradient Descent:
Gradient Descent is one such optimization algorithm. It has a very simple rule:
![]()
where
We use the above update rule when we have to maximize our cost function. To minimize our cost function, we have to move in the opposite direction of our gradients. So the update rule becomes:
![]()
Stochastic Gradient Descent:
As simple as Gradient descent seems, implementing it for huge datasets has its own problem. Why? The problem remains in the gradient ![]() . Let me explain, for most applications we define cost function something like this:
. Let me explain, for most applications we define cost function something like this:
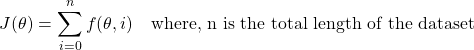
If we had a dataset of length 1000, then we find
Stochastic Gradient Descent comes here for the rescue. SGD says that we can estimate the true gradient using gradient at each instance and if we estimate for a large number of instances we can come pretty close to true gradients. This allows working with batches when we have huge datasets.
Note: Gradient descent will take you directly to maxima or minima. SGD will wander here and there, but if repeated correctly, over time it will take you to the same place or at least some place near it.
Appendix C: Chain Rule:
You can actually think of the Cost function as a function of functions. Using notation ![]() as the output of node i and considering output node as node 5, we can say:
as the output of node i and considering output node as node 5, we can say:
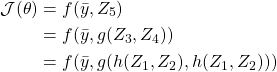
here ![]()
Chain Rule helps in finding gradients of composite functions such as ![]() . Multivariate chain rule says,
. Multivariate chain rule says,
(1) ![]()
Now we can use the chain rule to find ![]()
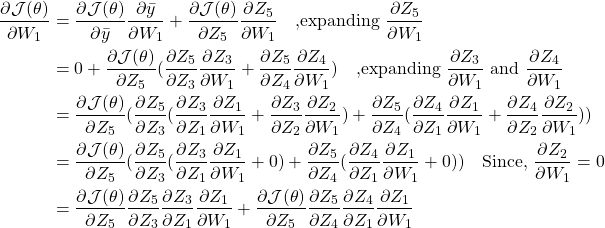
Appendix D: Jacobian and problem with their size:
Jacobian is a matrix which contains first-order partial derivatives of 2 vectors(even multidimensional vectors). Let’s say you have 2 vectors ![]() , then the jacobian is
, then the jacobian is ![]() , specifically:
, specifically:
(2) 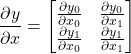
It tells how each element of x affects an element of y.
To show how Jacobians can be huge, let’s take the MLP we defined in the first gif.
So the size of different Jacobians we will use to compute gradients of
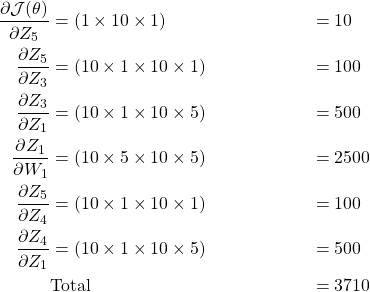
We will have to find 3710 scalar values in order to find gradients of 10×5= 50 scalar values. So, you can see that finding gradients using jacobians is not a feasible approach, especially when we increase the number of layers of increase the dimensions of our parameters.
Appendix E: Gradients in Autodiff
Especially notice ![]() since it has 2 children.
since it has 2 children.



Pingback: RNN, LSTM, GRU and Attention – Akash