The main goal behind this post is to look at the above NLP concepts. These concepts may be old but they are a stepping stone to understand the current SOA transformers which we will cover in a future post. We start with RNN.
RNN:
RNNs were originally motivated by the lack of ability of ANNs and MLP to model sequential data. They were initially used to model sequential data and they were good at it but only in short sequences. This is how a normal forward pass looks in a RNN.

When used with back-propagation (to read more on backpropagation check out this article.) RNNs have significant problems. The gradients tend to explode or vanish. Check out the next animation on the calculation of gradients in RNN backward pass.
As you can see, with each backward step through the RNN, the gradients keep getting multiplied by the term ![]() . If there were 10 steps, in the unrolling of RNN, the gradients passed to the parent module/network will be
. If there were 10 steps, in the unrolling of RNN, the gradients passed to the parent module/network will be ![]() . If
. If ![]() is a huge number then
is a huge number then ![]() will be enormous. Conversely, if
will be enormous. Conversely, if ![]() is a very small number then
is a very small number then ![]() will be minuscule. Hence for long sequences, the gradients tend to vanish or explode in RNNs.
will be minuscule. Hence for long sequences, the gradients tend to vanish or explode in RNNs.
LSTM:
LSTM improves upon RNN is 3 ways:
- It has a separate vector to save long-term dependencies.
- It has multiple operations within a cell.
- It solves the problem of vanishing and exploding gradients.
A great post on understanding LSTMs is this. The post explains LSTM in terms of computational steps and ‘gates’. I would take another approach. I will try to explain it intuitively. First, have a look at the next animation. It would help if you think of the Context Vector, C, as the memory of the system.
Essentially, operations in LSTM are about making changes to the memory and using memory with the input to get an output. Memory is stored in a vector, Context Vector, C. We call this vector a memory because the cell decides/reasons which things to keep in it and when to use it. In a supervised learning context, the cell decides to keep that information which maximizes the cost function. This decision or reasoning is done in small NNs or simple matrix transformations in 3 steps.
The 3 steps:
- Step 1, Remove/Forget parts of memory:
In LSTM, we are bounded by the amount of memory we can save. If we have a vector size of 100, then we can save 100 scalar values which aren’t enough if we want to model a sequence as long as a book. So, we need to keep forgetting old values that are no longer pertinent. The decision to remove which values is done by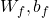 .
. ![Rendered by QuickLaTeX.com \begin{align*} f &= \sigma(W_f[h,x]+b_f)\\ C_1 &= f*C\end{align*}](https://akashe.io/wp-content/ql-cache/quicklatex.com-dcb1e92f04b6c57b91762a973f15fba9_l3.png)
where![Rendered by QuickLaTeX.com [h,x]](https://akashe.io/wp-content/ql-cache/quicklatex.com-ebecacb8daa8fd4064f2bba831a1fc08_l3.png) shows a concatenation of vectors
shows a concatenation of vectors 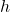 the hidden vector(covered in Step 3) and input
the hidden vector(covered in Step 3) and input 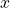 which represents new information. An important point is the usage of the sigmoid(
which represents new information. An important point is the usage of the sigmoid(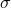 ). Sigmoid is a way of choosing the relative importance of each value in the context vector in the view of new information. A sigmoid value of
). Sigmoid is a way of choosing the relative importance of each value in the context vector in the view of new information. A sigmoid value of 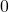 means the scalar value is no longer needed, a value of
means the scalar value is no longer needed, a value of 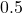 means that the scalar value needs to be halved and a value of
means that the scalar value needs to be halved and a value of 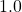 means keep the original context.
means keep the original context. - Step 2, Add information to memory:
As we model a sequence, we need to add information to context/memory based on the importance of the new information. Let’s say we encounter a new name in a sentence. The cell then decides if this new name is an important event. If it is, then the cell decides to add some information related to this event to the memory using an appropriate representation for the name.![Rendered by QuickLaTeX.com \begin{align*}i &= \sigma(W_i[h,x]+b_i) &&\quad\text{Cell deciding if input has something important?}\\C_{event} &= tanh(W_c[h,x]+b_c)&&\quad\text{New information representation}\\C_2 &= i*C_{event} && \quad\text{Selecting important parts of the representation}\\C_{new} &= C_1 + C_2 &&\quad\text{Adding selected parts to Context Vector}\end{align*}](https://akashe.io/wp-content/ql-cache/quicklatex.com-8f2f201a8c589aa464818a34c3a5871c_l3.png)
- Step 3, Get a new hidden vector:
A hidden vector also said as a hidden state is parts of memory that are important for output. We select these parts using the new information and last hidden vector. In most applications, the hidden vector is later used to predict some values. It is also used as an input to the cell at the next time step because it has important parts of memory wrt the last input.![Rendered by QuickLaTeX.com \begin{align*}o &= \sigma(W_o[h,x] + b_o) \\h_{new} &= o * tanh(C_{new})\end{align*}](https://akashe.io/wp-content/ql-cache/quicklatex.com-2dd5ee253e571078bd71ba57d25a6350_l3.png)
Note: I have removed timestep information from equations to make it more intuitive.
How LSTMs solve vanishing or exploding gradient?
The presence of a context vector acts as a residual connection in LSTM(though it is not a full residual connection). A context vector ![]() gets gradients from 2 directions.
gets gradients from 2 directions. ![]() and
and ![]() . The gradient from
. The gradient from ![]() and
and ![]() add up and is sent back towards
add up and is sent back towards ![]() . But before reaching
. But before reaching ![]() the gradient is multiplied by the output of Step 1(or forget gate). Since the output of Step 1 is a sigmoid it keeps the value between 0 and 1. This ensures gradients flow far back and all the trainable params get gradients from the context vector. But repeated multiplication with the output of Step 1 eventually makes the gradients negligible and that is why even LSTMs don’t work well very very long sequences.
the gradient is multiplied by the output of Step 1(or forget gate). Since the output of Step 1 is a sigmoid it keeps the value between 0 and 1. This ensures gradients flow far back and all the trainable params get gradients from the context vector. But repeated multiplication with the output of Step 1 eventually makes the gradients negligible and that is why even LSTMs don’t work well very very long sequences.
GRU:
An obvious question is why keep 2 separate vectors, context and hidden? Why can’t we directly use the context vector every time? The answer is GRU. GRU doesn’t have a separate context vector.

[Source: Understanding LSTM Networks]
GRU also does the 3 steps we discussed above. Removing information from memory, Adding information to memory, and getting a new hidden vector. The difference is how it achieves that.
Key differences with LSTM:
- It forgets only that part(
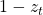 ) of the context which it updates(
) of the context which it updates(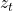 ).
). - It first chooses to forget some part(
 ) of the context. Then uses this ‘reset’ context(
) of the context. Then uses this ‘reset’ context(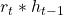 ) with input to form a new information representation.
) with input to form a new information representation. - It merges Step1 and Step2 of LSTM in a single step.
Seq2Seq
Sequence to Sequence is a type of encoder-decoder architecture. It is used in language translation, image captioning, conversational models, and text summarization. The encoder encodes sequential data to a vector. This vector is a representation of the entire sequential input data and is generally the hidden state of the encoder at the last encoder timestep. This vector is later used in a decoder as a starting representation. It uses the information in the vector to model another sequence. For e.g. in a language translation task, the source sentence is in one language and we want the decoder sequence to be a sentence in another language.
A typical seq2seq architecture looks like this.

Attention
An inherent problem with seq2seq architectures was the constraint of vector passed from encoder to decoder. Let’s say we had a source sentence of length 1000. By processing this sentence with an LSTM a lot of important context is lost by the time we reach the 1000th word. Attention is a nice solution to this problem. Simply put, attention enables the decoder to extract necessary information from all the encoder hidden states instead of relying only on the last hidden state.
Attention consists of 2 steps:
- Find out how much is the current decoder hidden state aligned with all the encoder hidden states?
Let’s define terms:
The encoder sequence length is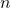 and decoder sequence length is
and decoder sequence length is 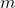 .
.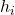 is the hidden state of the encoder at position
is the hidden state of the encoder at position 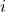 , where
, where 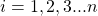
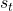 is the hidden state of the decoder at position
is the hidden state of the decoder at position 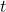 , where
, where 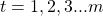
Now we have to find how each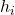 is correlated with each
is correlated with each 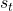 . To do so we find the quantity
. To do so we find the quantity  defined as
defined as
The function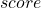 decides the correlation/alignment of
decides the correlation/alignment of 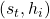 . Different forms of attention mechanism employ different
. Different forms of attention mechanism employ different  functions. A simple
functions. A simple  function would be a dot product
function would be a dot product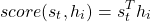
 [This figure shows the
[This figure shows the 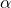 matrix of French sentence and its English Translation. Source: Bahdanau et al., 2015 ]
matrix of French sentence and its English Translation. Source: Bahdanau et al., 2015 ] - Give preference to encoder hidden states that are more aligned:
Now we define, context vector,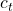 (Not to be confused with context vectors inside LSTMs). It depends on the last decoder hidden state
(Not to be confused with context vectors inside LSTMs). It depends on the last decoder hidden state 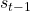 and the alignment score(
and the alignment score(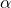 ) of
) of 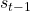 with all encoder hidden states
with all encoder hidden states 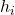 .
.
Preferably, we want our context vector,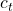 , to have more information from encoder hidden states it is aligned with. So we define,
, to have more information from encoder hidden states it is aligned with. So we define,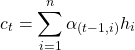
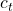 is the input to the decoder RNN/LSTM at timestep t. So based on the task, the decoder can decide which encoder hidden states to focus on using attention.
is the input to the decoder RNN/LSTM at timestep t. So based on the task, the decoder can decide which encoder hidden states to focus on using attention.


Wonderful explanation!
Thanks 🙂
Great work Akash!
Thanks Akshay.